Государство и право
Демография
История
Международные отношения
Педагогика
Политические науки
Психология
Религиоведение
Социология

3.3.1. Проектирование систем

  Общие понятия о проектировании. Если мы говорим о проектировании как о компоненте практической деятельности, то у Читателя, естественно, возникает вопрос - а что именно подлежит проектированию, что проектируется в этом случае? На этот вопрос есть ответ - речь идет о проектировании систем.
  Действительно, самое общее определение системы, которое дает Энциклопедический словарь [227]:
  - «система - множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство».
  Не противоречит этому определению более конкретное для нашего случая определение системы в системном анализе [192]:
  - «система - средство достижения цели; основные особенности систем: целостность, относительная обособленность от окружающей среды, наличие связей со средой, наличие частей и связей между ними (структурированность), подчиненность всей организации системы некоторой цели».
  С этих позиций под системой можно понимать и такие сложные объекты, как все народное хозяйство страны, или хозяйство какого-либо региона, или любое предприятие, организация, учреждение, так как они состоят из множества связанных между собой элементов, упорядоченных по отношениям и характеризующихся единством общих целей функционирования.
  Таким образом, мы имеем дело с иерархией систем. Так, на любом предприятии можно выделить технологическую компоненту, которая, в свою очередь, сама является системой - технологической системой; финансовую компоненту - финансовую систему; кадровую систему и т.д.
  Системой можно считать и очередной урок учителя в школе, и хирургическую операцию в больнице и т.д. Таким образом, образуется сложная иерархия систем: для каждой системы существует более общая система - надсистема; в то же время каждая система состоит из целой совокупности систем более низкого уровня - подсистем.
  Главным, системообразующим элементом любой проектируемой системы является ее цель. Как и сами системы, цели также образуют сложную иерархию.
  Объектом проектирования является та или иная система, в каждом конкретном случае своя.
  Понятия - проектирование, конструирование, моделирование, технология и т.д. - первоначально сформировались в сфере техники и индустрии. Впоследствии они были распространены в связи с развитием кибернетики на ряд других сфер - теорию управления, системный анализ и т.д. А потом они распространились повсеместно.
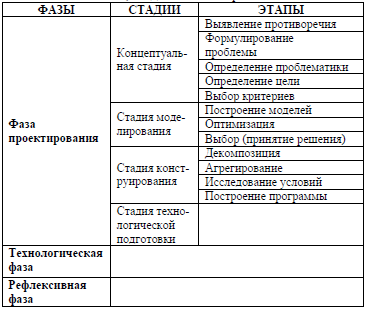
  Проектирование обычно рассматривается в последовательных стадиях, этапах его проведения. Разными авторами их состав и структура строятся по-разному (см. Табл. 9). Мы используем эти и другие публикации (например, [39, 192]), но при этом выстраиваем структуру стадий и этапов фазы проектирования, подчиняя ее общей логике организации процесса продуктивной практической деятельности. Эта структура выстраивается как бы в двойной логике одновременно: как последовательность действий проектирования, с одной стороны; и по уровням абстракции и конкретизации (сверху вниз) - с другой стороны.

Табл. 9. Последовательность системного анализа решения проблемы

  Итак, фаза проектирования включает следующие стадии – см. также Табл. 10 (в сравнении с Табл. 5) и Табл. 15 – Табл. 17:
  1. Концептуальная. Состоит из этапов: выявление противоречия; формулирование проблемы; определение проблематики; определение цели; выбор критериев.
  2. Моделирования. Состоит из этапов: построение моделей; оптимизация; выбор (принятие решения).
  3. Конструирования системы. Состоит из этапов: декомпозиция; агрегирование; исследование условий; построение
программы.
  4. Технологической подготовки.

Табл. 10. Фазы, стадии и этапы проекта

  Рассмотрим теперь содержание действий по стадиям и этапам.
  КОНЦЕПТУАЛЬНАЯ СТАДИЯ ПРОЕКТИРОВАНИЯ.
  Проектирование на концептуальной стадии начинается с этапа выявления противоречия: что мешает в практической деятельности отдельного специалиста, или предприятия, организации, или еще более крупной экономической, социальной, культурной системе и т.д. достичь высоких результатов? Или, по крайней мере, удовлетворительных результатов? Детальный анализ наличной ситуации позволяет, как правило, выявить целый клубок, комплекс противоречий. Среди них надо выделить основное, главное звено. Оно и составляет проблемную ситуацию, то есть такую ситуацию, когда неудовлетворительное состояние дел уже осознано, но пока неясно, что следует сделать для его изменения (этап формулирования проблемы).
  Приведем такой пример из области закупок авиалайнеров. Не только зарубежные, но и отечественные авиакомпании предпочитают покупать не наши отечественные самолеты, в частности, ТУ-154, а иностранные, в частности, аналог ТУ - Боинг 737 (проблема для нашей авиационной промышленности). Наши самолеты, как минимум, в 2 раза дешевле, по надежности, комфорту, не уступают Боингу. Аэродинамические качества значительно лучше - в воздухе наши самолеты редко «болтает», в отличие от зарубежных, при полете на которых то и дело раздается команда: «самолет попал в зону турбулентности, просим пристегнуть ремни». Были неэкономичные двигатели - их заменили на зарубежные - экономичные. Поставили импортную авионику. А самолеты все равно не покупают. Проблемная ситуация заключается, как выяснилось, в том, что среднесуточный налет ТУ - 5 часов (остальное время - регламентные и ремонтные работы). Среднесуточный налет Боинга - 15 часов. Таким образом, гораздо более дорогой самолет за счет большего налета окупается быстрее - вот это и составляет проблемную ситуацию.
  Этап определения проблематики. Любой специалист - практический работник или коллектив в социальных системах, экономических и других, совершая какие-либо новые более или менее крупные шаги, неизбежно затрагивает интересы других людей и организаций.
  Поэтому, в соответствии с принципом коммуникативности (см. выше) выделяется следующий этап: определения проблематики. Проблематика в системном анализе (см., например, [192]) определяется как сплетение, комплекс проблем, которые неразрывно связаны с проблемой, подлежащей разрешению. В методологии практической деятельности необходимость рассмотрения проблематики вытекает из того, что система практической деятельности включает в себя множество подсистем и входит в другие, более общие и сложные системы - надсистемы, а решение поставленной проблемы требует учета последствий для всех из них.
  Для определения проблематики необходимо охватить весь круг участников - физических лиц и организаций:
  1. Участников, принимающих решения, то есть тех, от полномочий которых непосредственно зависит решение проблемы (руководителей учреждения, фирмы и т.д., работников ведомственных или региональных органов управления и т.д.).
  2. Активных участников, чьи действия (содействия) потребуются при решении проблемы.
  3. Пассивных по отношению к решаемой проблеме участников, на ком скажутся (положительным или отрицательным образом) последствия решения проблемы.
  4. Участников с возможным негативным отношением к решению проблемы, которые могут предпринять враждебные действия.
  Каждый из участников может иметь свое видение проблемы, иметь свое отношение к ней, так как ее существование или исчезновение может привести к появлению у них их собственных проблем. Построение проблематики и состоит в определении (в т.ч. в описании) того, какие изменения и почему хочет (или не хочет) внести каждый из участников.
  Диалектический метод предписывает рассматривать проблему всесторонне, в том числе и во времени (историческом) и в пространственном плане. Проблематика, по сути дела, - это ответ на вопрос: какие существующие обстоятельства и прошлый опыт - как положительный, так и отрицательный - заставляют именно этих участников, именно в данной культурной среде, включающей именно данные ценности, именно в данный момент воспринимать данное состояние дел как проблему?
  Приведем такой пример. Содержание школьного общего среднего образования в течение уже многих десятилетий периодически перестраивается и обновляется - ведь построение содержания образования вполне резонно можно рассматривать как педагогический проект. Так вот, традиционно из раза в раз определение содержания школьного образования поручается работникам самой системы образования и ученым. А в решении проблемы содержания общего среднего образования заинтересовано все общество, все без исключения социальные, экономические и культурные структуры. И в решении этой проблемы должен участвовать очень широкий круг участников, из самых разных областей деятельности. Чего не происходит. Как известно, вопросы войны и мира нельзя позволять решать военным. Точно так же определять содержание школьного образования нежелательно поручать ученым и работникам сферы образования - они неизбежно будут отстаивать свои научные и корпоративные, а не всеобщие интересы.
  Другой пример. У нас много говорят и пишут о фермерстве в сельском хозяйстве, как о мощном рычаге его развития (проблема). Но фермерство, являясь образцом высочайшей продуктивности сельского хозяйства в США, Голландии, Австралии и других странах, в России в массовых масштабах, очевидно, не привьется. Так же, как не привилось оно в начале XX века, когда его пытался внедрить П.А. Столыпин. И дело здесь в национальных различиях менталитета. Фермер работает в одиночку. И это как нельзя лучше подходит к менталитету западноевропейского индивидуализма. Для российского общинного менталитета это не подходит. Так, столыпинские фермерские хозяйства поджигали сами крестьяне - «живи, как все, не высовывайся» (проблематика).
  Поэтому, например, организация колхозов в конце 20-х - начале 30-х годов XX в. не вызывала массового недовольства населения России - колхозы были близки традиционному общинному укладу российской деревни. Поэтому они и не распадаются в большинстве своем и сегодня при переходе к рыночной экономике - в отличие от совхозов, которые всегда «висели на шее» у государства.
  Таким образом, как видим, этап определения проблематики при проектировании систем отнюдь не прост, а иногда делает невозможным решение проблемы в желательном аспекте.
  Этап определения цели. Следующий этап концептуальной стадии проектирования - на основе сформулированной проблемы и установленной проблематики определяется цель проектирования системы. На данном важнейшем этапе определяется, что надо сделать для снятия проблемы - все последующие стадии и этапы проектирования будут определять - как это сделать.
  Основная трудность определения цели заключается в том, что, как уже говорилось выше, цель является как бы антиподом проблемы. Та или иная система создается для решения проблемы.
  При формулировании проблемы определяется, что является неудовлетворительным. Это относительно просто - ведь то, что нам не нравится, существует. Когда же мы переходим к цели, то пытаемся определить, что же нам хочется. При этом как бы указывается направление, в котором следует «уходить» от существующего и нас не устраивающего положения дел. Но таких возможных направлений много. А выбрать надо одно - правильное, рациональное. Точнее говоря - как правило, одно - из-за ограниченности ресурсов (временных, материальных, интеллектуальных и т.д.) «гнаться за двумя зайцами», чаще всего, не удается.
  Определение целей - чрезвычайно сложный и тонкий процесс. Это сочетание логики и интуиции. Д. Джонс, известный специалист по проектированию, отмечает, что в этом случае «пути ... сочетания интуитивного с рациональным не установлены; пожалуй, их и невозможно установить в общем виде, в отрыве от конкретной проблемы и конкретного человека, так как они зависят от того, какое количество объективной информации имеется в распоряжении проектировщика, а также от его квалификации и опыта» [62]. И, добавим еще, от его личных склонностей и вкусов.
  Ошибки в определении целей создания систем чрезвычайно часты повсеместно. Наиболее часто встречаются три их варианта:
  1. Когда цель ставится как самоцель, в отсутствии проблемы или при неопределенной, не сформулированной проблеме. Ярким примером цели как самоцели является история развития экономики бывшего СССР. В конце 20-х годов прошлого века была поставлена общегосударственная цель: «догнать и перегнать ведущие капиталистические страны по выпуску основных видов промышленной и сельскохозяйственной продукции». И на выполнение этой цели была нацелена вся экономика страны вплоть до конца существования СССР. Не на реализацию, не на потребление, а именно на выпуск.
  И эта «цель» - самоцель была достигнута. Страна добывала нефти и газа больше всех в мире - но «лишний» бензин водители сливали в канавы. Выплавлялось больше всех стали - а в магазинах не было бритвенных лезвий. Выпускалось металлорежущих станков и зерноуборочных комбайнов в 15 раз больше, чем в США, тракторов в 6 раз больше, чем в США - в результате на заводах и в колхозах скопились гигантские свалки металлолома - а населению купить легковой автомобиль было практически невозможно. Картофеля выращивалось больше, чем в США, Англии и Германии вместе взятых, поголовье скота было в 3 раза больше, чем в США, а в магазинах не было молока и мяса. И так далее. Последствия достижения такой самоцели мы наблюдаем сейчас.
  2. Подмена цели средствами. Рассмотрим в качестве примера введение системы страховой медицины, которая должна была стать средством улучшения медицинского обслуживания населения (как цели). Фактически же система страхования превратилась в цель: страховые компании наживаются, в поликлиниках и больницах стали различать «выгодные и невыгодные» (для них, а не для больных) анализы, процедуры, операции и т.п., а человек, оказавшийся по каким-либо причинам в другом городе - командированный, мигрант, отдыхающий - вообще не может получить бесплатную медицинскую помощь - его медицинский полис «из другой страховой компании».
  Другой пример. Автор (А.Н.) когда-то проверял профтехучилища в городе Жданове - теперь Мариуполь, Украина. Там было построено пять самых современных по тому времени училищ - вполне достаточное количество для этого города. Но все они были построены в одном микрорайоне. А город раскинут на огромной территории со многими отдаленными друг от друга микрорайонами. Типичный случай: цель фактически должна была заключаться в обеспечении доступности профессионального образования для молодежи. В том числе, транспортной доступности. Но сформулировали цель по-другому: построить училища, что на самом деле было средством, а не целью. В результате построенные училища по большей части пустовали, молодежь из других микрорайонов «болталась» на улице, а промышленные предприятия имели острую нехватку квалифицированной рабочей силы.
  3. Смешение целей. Всегда существует опасность ошибочно принять другие цели, чем на самом деле необходимо. Такая ситуация нередко возникает, в частности, когда специалисты-профессионалы, участвующие в решении проблем, навязывают свое видение мира и тем самым подменяют главные цели своими [192]. «Операция прошла успешно, но пациент умер» - это не злая шутка, а действительно встречающееся среди хирургов высказывание. Многие примеры смешения целей хорошо известны - это трагедии Арала, Кара-Богаз- Гола, проекта работ по переброске вод северных рек на юг и т.д. Широкое распространение явления смешения целей стало даже поводом для большой серии анекдотов о неосмотрительно сформулированном техническом задании. А. Эйнштейн как-то на вопрос о том, что, по его мнению, станет главной проблемой в конце XX века, ответил: «Совершенство средств и смешение целей». Очевидно, так оно и вышло.
  Так, в конце 80-х гг. прошлого века встала проблема создания отечественного персонального компьютера, причем, правительство на это выделяло огромные ассигнования. Вместо того, чтобы создать одну модель, совместимую с общемировой версией IBM, три союзных министерства: Минэлек- тронпром, Минприбор и Минрадиопром, отстаивая в конкурентной борьбе за государственные ассигнования свои ведомственные интересы, а в составе этих министерств различные заводы, отстаивая свои заводские интересы, стали выпускать целый «зоопарк» разномастных компьютеров: «Агаты», «Микроши», «Искры», «Корветы», УКНЦ и т.д. и т. п., для которых почти не было программного обеспечения. В результате информатизация страны была задержана минимум на десятилетие, а отечественная электронная промышленность до сих пор не может оправиться от провала.
  Таким образом, необходимо очень внимательно подходить к определению целей. Так как правильно заданная цель - это половина успеха в решении проблемы.
  Если цели, как правило, задаются на качественном уровне, то в некотором смысле замещением их на количественном уровне являются критерии. Поэтому следующим этапом на концептуальной стадии проектирования является выбор критериев.
  Этап выбора критериев. Как в научноисследовательской работе, так и в практической деятельности, одним из наиболее острых и сложных вопросов является выбор критериев.
  Содержание вопроса перехода от целей к критериям становится ясным, если рассматривать критерии как количественные модели качественных целей. Действительно, сформированные критерии в дальнейшем как бы в некотором смысле замещают цели. От критериев требуется возможно большее соответствие целям, сходство с ними. Но в тоже время критерии не могут полностью совпадать с целями, поскольку они фиксируются по-разному. Цели просто называются. А критерии должны быть выражены в тех или иных шкалах измерения (кроме, естественно, шкалы наименований - см. выше главу 2).
  Критерии эффективности - важнейшая проблема вообще в любой деятельности. Из-за ошибочного выбора критериев неоднократно происходили крушения целых социальных институтов и экономических систем. Часто приводится такой классический пример неправильного выбора критерия и вызванных этим последствий: в двадцатые годы нашего столетия пожарным, чтобы они «меньше спали», была установлена заработная плата, пропорциональная числу потушенных за месяц пожаров. В итоге дело кончилось тем, что пожарные сами стали устраивать поджоги!
  Другой классический пример ошибки в выборе критерия. Во время Второй мировой войны в Англии, подвергшейся массированным налетам фашистской авиации, остро не хватало зенитных орудий. Но поскольку Англия - островная страна, у нее был огромный торговый флот, а каждое судно было снабжено двумя зенитками. Когда выяснилось, что судовые зенитки не сбили ни одного вражеского самолета, генералы тут же приказали поснимать их с судов торгового флота и передать их на сушу. Но количество потопленных бомбами судов тут же возросло в 6 раз! Оказалось, что задача зенитных орудий на судах была не в том, чтобы сбивать самолеты, а в том, чтобы отпугивать их и не давать бомбить суда прицельно.
  Критерии, по сути дела, отображают системы ценностей. Но системы ценностей, как правило, бывают различными: философскими, психологическими, моральными, политическими, экономическими, эстетическими и т.д., которых в каждой конкретной ситуации человек или организация придерживаются одновременно - в полном или частичном наборе. Эти системы ценностей несводимы друг к другу, и чаще всего несравнимы между собой. Отсюда вытекает многокри- териальность большинства практических задач, и, таким образом, при решении практических проблем построение критериев является скорее искусством, чем наукой.
  Многокритериальность реальных задач связана с тем, что одну цель, как правило, не удается выразить одним критерием. Возможны, конечно, случаи, когда единственный критерий отвечает требованиям практики. Так, надежность авиаперевозок однозначно определяется статистикой аварий и катастроф. Или, например, по стандартам ООН уровень жизни в разных странах сравнивается по годичному среднедушевому доходу, пересчитанному на доллары США; уровень медицинского обслуживания - по статистике детской смертности; уровень образования в стране - так называемый коэффициент интеллектуализации населения - по среднему числу лет, проведенному каждым жителем страны в учебных заведениях. Но, естественно, эти критерии несколько условны.
  В целом, случаи, когда единственный критерий удачно отображает цель, весьма редки. Так, заработанная плата школьного учителя установлена в прямо пропорциональной зависимости от количества проведенных уроков. Но количество проведенных уроков никак не характеризует качество обучения и воспитания учащихся! Объем расходов на одного ученика не оценивает качества обучения в школе; число студентов на одного преподавателя совсем не однозначно связано с качеством подготовки специалистов в ВУЗе и т. д.
  Решение может состоять или в поиске более адекватного критерия, если он существует, или в использовании нескольких критериев, описывающих одну цель по-разному и дополняющих друг друга. В [192] приводится интересный опыт формирования критериев для достаточно ясной цели: улучшить уборку мусора в большом городе. В результате анализа были отвергнуты как неадекватные следующие, на первый взгляд, подходящие критерии: расходы по уборке мусора в расчете на одну квартиру, число тонн убираемого мусора в расчете на один рабочий человеко-час, общий вес вывозимого мусора - эти критерии ничего не говорят о качестве работы. Более удачными были признаны такие критерии, как процент жилых кварталов без заболеваний, снижение числа пожаров из-за возгорания мусора, уменьшение числа укусов людей крысами, количество обоснованных жалоб жителей на скопление мусора. Но, очевидно, что и эти критерии отражают лишь отдельные стороны качества уборки мусора в городе.
  Зачастую критерии бывает целесообразно разнести по трем составляющим:
  - цель проектируемой системы;
  - средства и способы ее реализации;
  - отношения системы со средой.
  Причем, нередко критерии могут входить в противоположные отношения. Так, при проектировании автомобиля одной из целей является повышение его комфортабельности, но это ведет к увеличению его стоимости. Повышение комфорта требует увеличения габаритов автомобиля, но тогда возникают сложности с его парковкой, что будет относиться к «отношениям со средой».
  Часто многие актуальные проблемы не могут быть решены из-за отсутствия более или менее четких и достоверных критериев. Примером является сегодняшняя система приема абитуриента в ВУЗы, которая никого не удовлетворяет. Всем понятно, что оценки за вступительные экзамены по предметам никак не характеризуют потенциальные возможности будущего специалиста - сможет ли он стать хорошим учителем, врачом, инженером, финансистом и т.д. Ведь школьные знания не характеризуют ни способностей абитуриента, ни его интересов и склонностей. Но других-то достоверных критериев, чтобы можно было точно сказать - этот юноша в будущем будет талантливым хирургом, а эта девушка - будущий министр финансов - просто нет. Поэтому описанная проблема на сегодня нерешаема.
  Наиболее распространенными при анализе, в частности, экономических и технических систем являются следующие критерии: финансовые (прибыль, стоимость и т.д.), объемные показатели (измеряющие количество продукта), технические качества: эффективность функционирования, надежность и т.д., живучесть, совместимость с уже существующими системами, приспособляемость, гибкость, стойкость против морального старения, безопасность и т.д. Такие критерии, безусловно, полезны. Но их следует рассматривать скорее как основу для конкретного поиска в каждом конкретном случае.
  Отметим, что термин «оценка» используется в двух значениях - как результат «измерения», и как процесс. Процесс оценки, вкратце, заключается в следующем. Состояние системы описывается некоторыми показателями, измеряемыми в соответствующих шкалах. Эффективность функционирования системы оценивается по некоторым критериям, оценки по которым («оценка» - как результат) также измеряются в соответствующих шкалах. Процесс оценки заключается в переходе из пространства состояний системы в критериальное пространство - см. Рис. 15 (причем обычно m ≤ n), то есть, в установлении зависимости между значениями оценок по критериям и значениями показателей состояния системы (в частном случае критерии могут совпадать с показателями). При этом выбор критериев обычно диктуется целями оценки.
  Приведем пример из физики. В модели идеального газа состояние системы (множества молекул газа, заключенного в некоторый сосуд) характеризуется такими показателями (микропараметрами) как координаты и скорости всех молекул газа. Размерность пространства состояний чрезвычайно высока (n ≈ 10²⁴ ). Процесс оценки, производимый в целях компактного описания рассматриваемой системы, заключается в переходе к агрегированному пространству критериев (макропараметров): давление, объем и температура (m = 3).

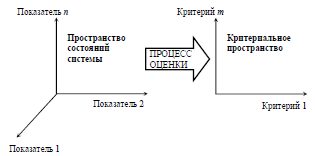
Рис. 15. Процесс оценки

  Второй пример - из экономики. Состояние такой системы, как экономика некоторого региона, может описываться множеством показателей - число предприятий и организаций в той или иной отрасли народного хозяйства, финансовые и производственные результаты деятельности каждого из них и т.д. Оценка данной системы, производимая с целью определения перспективных направлений развития экономики региона, будет заключаться в переходе к набору критериев, выбор которых зависит от того, какой смысл вкладывается в «перспективность». Если речь идет об увеличении регионального валового продукта, то целесообразно использовать такой критерий, как отдача на единицу инвестируемых средств. Если под перспективностью понимать рост числа рабочих мест, то критерии будут другими; если неухудшение экологической обстановки - то третьими, и т. д.
  Определением цели и критериев завершается первая, концептуальная стадия проектирования систем. Формой документа, где отражаются цели и критерии (если он необходим) является техническое задание. Название для специалистов гуманитарных сфер, прямо скажем, режет слух. Но эта форма документа распространилась повсеместно и уже достаточно широко используется во всех областях.
  СТАДИЯ МОДЕЛИРОВАНИЯ. Следующей стадией фазы проектирования системы становится ее моделирование, заключающееся в построении, анализе и оптимизации моделей. Приведем, сначала, определения модели:
  Модель - в широком смысле - любой образ, аналог (мысленный или условный: изображение, описание, схема, чертеж, график, план, карта и т.п.) какого-либо объекта, процесса или явления (оригинала данной модели) [227, Статья «Модель», 5-е значение];
  Моделью можно назвать искусственно создаваемый образ конкретного предмета, устройства, процесса, явления (и, в конечном счете, любой системы) [59];
  Оба этих определения не противоречат друг другу. В нашем случае модель выступает как образ будущей системы. В процессе моделирования задействованы как бы четыре «участника»: «субъект» - инициатор моделирования и/или пользователь его результатов; «объект-оригинал» - предмет моделирования, то есть та система, которую хочет создать и/или пользоваться в дальнейшем «субъект»; «модель» - образ, отображение; «среда», в которой находятся и с которой взаимодействуют все участники. Как известно, модели делятся на познавательные и прагматические («практические») [192], а также, добавим, художественные (см. главу 4).
  В целях уяснения сущности моделирования сопоставим стадию моделирования в проектировании систем в практической деятельности с проектированием научного исследования (научная деятельность). Познавательные модели - это предположительные образы будущего научного знания, то есть научные гипотезы. И стадии моделирования в практической деятельности, в проектировании научного исследования соответствует стадия построения гипотезы. Таким образом, познавательные модели отражают предположительно существующее (научное знание). Прагматические же модели - не существующее (в практике), но желаемое и, возможно, осуществимое.
  Прагматические модели проектируемых систем, так же, как и сами системы, могут быть, естественно, на разных уровнях иерархии. Можно говорить, к примеру, о модели урока в школе, о модели какого-либо предприятия, фирмы, о региональной модели здравоохранения, о модели железнодорожного транспорта страны и т.д.
  Прагматические модели являются способом организации практических действий, способом представления как бы образцово правильных действий и их результатов, то есть являются рабочим представлением, мысленным образцом будущей системы. Таким образом, прагматические модели носят нормативный характер для дальнейшей деятельности, играют роль стандарта, образца, под который «подгоняется» в дальнейшем как сама деятельность, так и ее результаты. Примерами прагматических моделей могут быть планы и программы действий, уставы организаций, кодексы законов, рабочие чертежи, экзаменационные требования и т.д.
  Стадия моделирования включает в себя этапы:
  - построения моделей;
  - оптимизации;
  - выбора (принятия решения).
  Этап построения моделей. Для создания моделей у человека есть всего два типа «материалов» - средства самого сознания и средства окружающего материального мира. Соответственно этому модели делятся на абстрактные (идеальные) и материальные (реальные, вещественные).
  Абстрактные модели являются идеальными конструкциями, построенными средствами мышления, сознания.
  Абстрактные модели являются языковыми конструкциями. Абстрактные модели могут формироваться и передаваться другим людям средствами разных языков, языков разных уровней специализации.
  Во-первых, посредством естественного языка (как конечный результат, поскольку в процессе построения моделей человеком используются и неязыковые формы мышления - «интуиция», образное мышление и т.д.). На естественном языке человек может говорить обо всем, он является средством построения любых абстрактных моделей. Универсальность естественного языка достигается еще и тем, что языковые модели обладают неоднородностью, расплывчатостью, размытостью. Многозначность почти каждого слова, используемого в естественном языке любой национальности, а также неопределенность слов (несколько, почти, много и т.д.) при огромном числе вариантов их соединения во фразы позволяет любую ситуацию отобразить с достаточной для обычных практических целей точностью. Эта приблизительность является неотъемлемым свойством языковых моделей. Но рано или поздно практика сталкивается с ситуациями, когда приблизительность естественного языка оборачивается недостатком, который необходимо преодолевать.
  Поэтому, во-вторых, для построения абстрактных моделей используются «профессиональные» языки. Их применяют люди, связанные общими для них, но частными для всех остальных людей видами деятельности. Наиболее ярко это проявляется на примере языков конкретных отраслей наук сильной версии (см. раздел 1.2). Дифференциация наук объективно потребовала создания специализированных языков, более четких и точных, чем естественный.
  В-третьих, когда средств естественного и профессионального языков не хватает для построения моделей, используются искусственные, в том числе формализованные, языки - например, в логике, математике. К искусственным языкам относятся компьютерные языки, а также чертежи, схемы и т.п.
  В результате получается иерархия языков и соответствующая иерархия типов моделей. На верхнем уровне этого спектра находятся модели, создаваемые средствами естественного языка, и так вплоть до моделей, имеющих максимально достижимую определенность и точность для сегодняшнего состояния данной отрасли профессиональной деятельности. Наверное, так и следует понимать известные высказывания И. Канта и К. Маркса о том, что любая отрасль знания может тем с большим основанием именоваться наукой, чем в большей степени в ней используется математика. Математические (в строгом смысле) модели обладают абсолютной точностью. Но чтобы дойти до их использования в какой-либо области, необходимо получить достаточный для этого объем достоверных знаний. Нематематизированность многих общественных и гуманитарных не означает их нена- учности, а есть следствие познавательной сложности их предметов. В них модели строятся, как правило, с использованием средств естественного языка.
  Функции моделирования. Можно выделить следующие функции моделирования:
  - дескриптивная функция;
  - прогностическая функция;
  - нормативная функция.
  Дескриптивная функция заключается в том, что за счет абстрагирования модели позволяют достаточно просто объяснить наблюдаемые на практике явления и процессы (другими словами, они дают ответ на вопрос «почему мир устроен так»). Успешные в этом отношении модели становятся компонентами научных теорий и являются эффективным средством отражения содержания последних (поэтому познавательную функцию моделирования можно рассматривать как составляющую дескриптивной функции).
  Прогностическая функция моделирования отражает его возможность предсказывать будущие свойства и состояния моделируемых систем (см. также обсуждение методов прогнозирования выше), то есть отвечать на вопрос «что будет?».
  Нормативная функция моделирования заключается в получении ответа на вопрос «как должно быть?» - если, помимо состояния системы, заданы критерии оценки ее состояния, то за счет использования оптимизации (см. ниже) возможно не только описать существующую систему, но и построить ее нормативный образ - желательный с точки зрения субъекта, интересы и предпочтения которого отражены используемыми критериями.
  Нормативная функция моделирования тесно связана с решением задач управления (см. ниже), то есть, ответе на вопрос «как добиться желаемого (состояния, свойств системы и т.д.)?».
  Требования, предъявляемые к моделям. Для того, чтобы создаваемая модель соответствовала своему назначению, недостаточно создать просто модель. Необходимо, чтобы она отвечала ряду требований, обеспечивающих ее функционирование. Невыполнение этих требований лишает модель ее модельных свойств.
  Первым таким требованием является ее ингерентность, то есть достаточная степень согласованности создаваемой модели со средой, чтобы создаваемая модель (в соответствии с принципом коммуникативности - см. выше) была согласована с культурной средой, в которой ей предстоит функционировать, входила бы в эту среду не как чужеродный элемент, а как естественная составная часть [39].
  Другой аспект ингерентности модели состоит в том, что в ней должны быть предусмотрены не только «стыковочные узлы» со средой (интерфейсы), но, и, что не менее важно, в самой среде должны быть созданы предпосылки, обеспечивающие функционирование будущей системы. То есть не только модель должна приспосабливаться к среде, но и среду необходимо приспосабливать к модели будущей системы. Так, например, проблема внедрения банковских карт и банкоматов заключается не только в том, чтобы изготовить карты и повсеместно установить банкоматы, но и в том, чтобы научить и приучить население пользоваться ими.
  Второе требование - простота модели. С одной стороны, простота модели - ее неизбежное свойство: в модели невозможно зафиксировать все многообразие реальной ситуации. Ведь, допустим, школьный учитель, строя модель урока, не может предусмотреть всего невообразимого множества возможных ситуаций, которые могут иметь место в процессе проведения урока - он всегда оставляет определенную возможность, свободу маневра - перекладывая все возможное потенциальное многообразие на импровизацию.
  С другой стороны, простота модели неизбежна из-за необходимости оперирования с ней, использования ее как рабочего инструмента, который должен быть обозрим и понятен, доступен каждому, кто будет участвовать в реализации модели. Поясним этот аспект таким банальным примером: любой документ, направляемый руководству, как показывает опыт, не должен содержать более 1,5 страниц текста - длинные документы «начальство» просто не читает: у «начальства» слишком ограниченный временный ресурс, на большие тексты у крупных руководителей просто нет времени.
  С третьей стороны, есть еще один, довольно интересный и непонятный пока аспект требования простоты модели, который заключается в том, что чем проще модель, тем она ближе к моделируемой реальности и тем она удобнее для использования. Классический пример - геоцентрическая модель Птолемея и гелиоцентрическая модель Коперника. Обе модели позволяют с достаточной точностью вычислять движение планет, предсказывать затмения солнца и т.п. Но модель Коперника истинна и намного проще для использования, чем модель Птолемея. Ведь недаром древние подметили, что простота - печать истины. У физиков, математиков, к примеру, есть довольно интересный критерий оценки решения задач: если уравнение простое и «красивое» - то оно, скорее всего, истинно. Авторы данной книги могут привести примеры участия в экспертизе самых разнообразных проектов: приходилось неоднократно убеждаться, что если в качестве проекта попадается многостраничный документ со сложной запутанной структурой и «красноречивыми» мудреными фразами - то, совершенно очевидно, не читая до конца, можно сказать - это пустое. И наоборот. Краткий, четкий документ с весьма ограниченным набором позиций, но хорошо логически структурированных, заслуживает пристального внимания.
  Можно привести и другой пример. В книге нобелевского лауреата Г. Саймона [218] рассматривается следующая ситуация. Предположим, что мы наблюдаем за тем, как муравей движется по песку из одной точки в другую. Целью муравья может быть стремление минимизировать затраты своей энергии, поэтому он огибает горки песка. Его «целевая функция» характеризует зависимость затрат энергии, которые он хочет минимизировать, от рельефа (внешней среды), и от его траектории (действия). Пусть мы наблюдаем только проекцию на горизонтальную плоскость траектории муравья. Если рельеф, по которому двигался муравей, неизвестен, то объяснить поведение муравья (сложную, петляющую траекторию) довольно непросто, и придется строить весьма хитроумные модели. Но если «угадать», что цель муравья проста, и включить в модель «рельеф», то все существенно упростится. По аналогии Г. Саймон выдвигает гипотезу, что наблюдаемое разнообразие и сложность поведения людей объясняются не сложностью принципов принятия ими решений (выбора действий), которые сами по себе просты, а разнообразием ситуаций (состояний внешней среды), в которых принимаются решения. С этим мнением вполне можно согласиться. Вопрос только в том, как найти эти простые принципы?
  Наконец, третье требование, предъявляемое к модели - ее адекватность. Адекватность модели означает возможность с ее помощью достичь поставленной цели проекта в соответствии со сформулированными критериями (см. также Рис. 19 и обсуждение проблем адекватности математических моделей ниже). Адекватность модели означает, что она достаточно полна, точна и истинна. Достаточно не вообще, а именно в той мере, которая позволяет достичь поставленной цели. Иногда удается (и это желательно) ввести некоторую меру адекватности модели, то есть определить способ сравнения разных моделей по степени успешности достижения цели с их помощью.
  Таким образом, мы выделили три основных требования, предъявляемых к моделям (см. Рис. 16): ингерентности, простоты и адекватности как отношения моделей с тремя остальными «участниками» процесса моделирования: со средой (ингерентность), с субъектом, создающим и/или использующим модель (простота), с моделируемым объектом, то есть с создаваемой системой (адекватность).

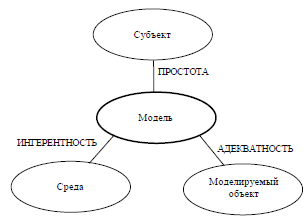
Рис. 16. Требования, предъявляемые к моделям

  Методы моделирования. Методы моделирования систем можно разделить на два класса. Называются эти классы в разных публикациях по-разному:
  - методы качественные и количественные. Смысл разделения понятен. Однако такое разделение не совсем точно, поскольку качественные методы могут сопровождаться при обработке получаемых результатов и количественными представлениями, например с использованием средств математической статистики;
  - методы, использующие средства естественного языка, и методы, использующие специальные языки. Смысл разделения также понятен, но тоже не совсем точен, поскольку гра- фические методы (схемы, диаграммы и т.д.) в первый класс не попадают, но широко используются в практике;
  - методы содержательные и формальные. Тоже не точно, поскольку компьютерное моделирование может требовать минимальной формализации.
  И так далее .
  Существует множество более детальных классификаций моделей и/или видов моделирования. Например, на Рис. 17 приведена система классификаций видов моделирования, заимствованная из [226].

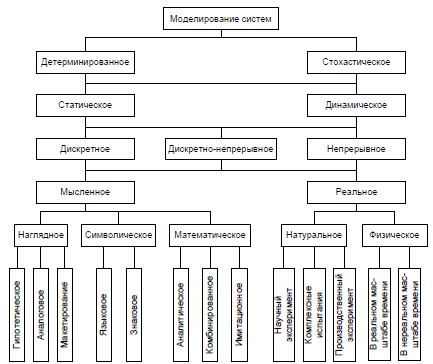
Рис. 17. Система классификаций видов моделирования

  Качественные методы моделирования. Рассмотрим некоторые качественные методы моделирования. Наиболее распространенным «качественным» методом моделирования, применяемым, в том числе, в рамках комплексного прогнозирования [221], является метод сценариев.
  Метод «сценариев». Метод подготовки и согласования представлений о проектируемой системе, изложенных в письменном виде, получил название метода «сценариев». Первоначально этот метод предполагал подготовку текста, содержащего логическую последовательность событий или возможные варианты решения проблемы, развернутые во времени. Однако позднее обязательное требование временных координат было снято, и сценарием стал называться любой документ, содержащий анализ рассматриваемой проблемы и предложения по ее решению, по развитию системы, независимо от того, в какой форме он представлен.
  Как правило, на практике предложения для подготовки подобных документов пишутся экспертами вначале индивидуально, а затем формируется согласованный текст.
  Сценарий требует не только содержательных рассуждений, помогающих не упустить детали, но и содержит, как правило, результаты количественного техникоэкономического и/или статистического анализа с предварительными выводами. Группа экспертов, подготавливающая сценарий, пользуется обычно правом получения необходимых сведений от тех или иных организаций, необходимых консультаций.
  Роль специалистов при подготовке сценария - выявить общие закономерности развития системы; проанализировать внешние и внутренние факторы, влияющие на ее развитие и формулирование целей; провести анализ высказываний ведущих специалистов в периодической печати, научных публикациях и других источниках информации; создать вспомогательные информационные фонды, способствующие решению соответствующей проблемы.
  Сценарии представляют ценность для лиц, принимающих решения, только тогда, когда они не просто являются плодом фантазии, а представляют собой логически обоснованные модели будущего, которые после принятия решения можно рассматривать как прогноз, как приемлемый рассказ о том, «что случится, если ...».
  Создание сценариев представляет собой творческую работу. В этой области накоплен определенный опыт, имеются свои эвристики. Например, рекомендуется разрабатывать «верхний» и «нижний» (или «оптимистический» и «пессимистический») сценарии - как бы крайние случаи, между которыми может находиться возможное будущее. Такой прием позволяет отчасти компенсировать или явно выразить неопределенности, связанные с предсказанием будущего. Иногда полезно включать в сценарий воображаемый активно противодействующий элемент, моделируя тем самым «наихудший случай». Кроме того, рекомендуется не разрабатывать детально (как ненадежные и непрактичные) сценарии, слишком «чувствительные» к небольшим отклонениям на ранних стадиях. Важными этапами создания сценариев являются: составление перечня факторов, влияющих на ход событий, со специальным выделением лиц, которые контролируют эти факторы прямо или косвенно.
  В последнее время понятие сценария расширяется в направлении как областей применения, так и форм представления и методов их разработки: в сценарий вводятся количественные параметры и устанавливаются их взаимозависимости, предлагаются методики подготовки сценария с использованием компьютеров, методики целевого управления подготовкой сценария (см. обзор методов экспертного прогнозирования в [221]).
  Сценарий позволяет создать предварительное представление о системе. Однако сценарий - это все же текст со всеми вытекающими последствиями (синонимия, омонимия, парадоксы), обусловливающими возможность неоднозначного его толкования. Вспомним Ф. Тютчева: «Мысль изреченная есть ложь». Поэтому его следует рассматривать как основу для дальнейшей разработки модели.
  Графические методы. Графические представления позволяют наглядно отработать структуру моделируемых систем и процессов, происходящих в них. В этих целях используются графики, схемы, диаграммы, гистограммы, древовидные структуры и т.д. Дальнейшим развитием графических методов стало использование, в частности, теории графов и возникших на ее основе методов календарносетевого планирования и управления [26, 39 и др.] - см. ниже.
  Метод структуризации. Структурные представления разного рода позволяют разделить сложную проблему с большой неопределенностью на более мелкие, лучше поддающиеся анализу, что само по себе можно рассматривать как некоторый метод моделирования, именуемый иногда системно-структурным. Виды структур, получаемые путем расчленения системы во времени - сетевые структуры или в «пространстве» - иерархические структуры, матричные структуры. В качестве особого метода структуризации можно выделить метод «дерева целей».
  Метод «дерева целей». Идея метода дерева целей была предложена У. Черчменом в связи с проблемами принятия решений в промышленности [264]. Термин «дерево» подразумевает использование иерархической структуры, получаемой путем расчленения общей цели на подцели, а их, в свою очередь, на более детальные составляющие, которые в конкретных приложениях называют подцелями нижележащих уровней, направлениями, задачами проблемами, а начиная с некоторого уровня - функциями. Как правило, термин «дерево целей»используется для иерархических структур, имеющих отношения строгого (древовидного) порядка, но иногда применяется и в случае «слабых» иерархий. Поэтому более правильным является термин В.М. Глушкова «прогнозный граф», однако в силу истории возникновения метода более распространен термин «дерево целей».
  Морфологический метод. Термином «морфология» в биологии и языкознании определяется учение о внутренней структуре исследуемых систем (организмов, языков) или сама внутренняя структура этих систем. Идея морфологического способа мышления восходит к Аристотелю и Платону. Однако в систематизированном виде методы морфологического анализа сложных систем были разработаны швейцарским астрономом (венгром по происхождению) Ф. Цвикки, и долгое время морфологический подход к исследованию и проектированию сложных систем был известен под названием метода Цвикки [39, 192 и др.]. Основная идея морфологического подхода - систематически находить наибольшее количество, а в пределе все возможные варианты реализации системы путем комбинирования основных выделенных структурных элементов или их признаков. При этом система или проблема может разбиваться на части разными способами и рассматриваться в различных аспектах.
  Все вышеперечисленные методы могут использоваться как отдельными специалистами, так и коллективами. Следующая группа методов относится к методам коллективного (группового) моделирования. Как правило, они направлены на то, чтобы включить в рассмотрение на этом этапе как можно больше возможных вариантов построения моделей - так называемое генерирование альтернатив.
  Деловые игры. Деловыми играми называется имитационное моделирование реальных ситуаций, в процессе которого участники игры ведут себя так, будто они в реальности выполняют порученную им роль, причем сама реальность заменяется некоторой моделью. Примерами являются штабные игры и маневры военных, работа на тренажерах различных операторов технических систем (летчиков, диспетчеров электростанций и т.д.), административные игры и т. п. Несмотря на то, что чаще всего деловые игры используются для обучения, их можно использовать и для экспериментального генерирования альтернатив создаваемых моделей. Важную роль в деловых играх кроме участников играют контрольноарбитражные группы, управляющие созданием моделей, регистрирующие ход игры и обобщающие ее результаты [53, 54 и др.].
  К методам коллективного моделирования также можно отнести метод мозгового штурма, метод «Делфи» и метод синектики [62, 126, 235, 257 и др.]
  Метод мозгового штурма специально разработан для получения максимального количества предложений при создании моделей.
  Техника мозгового штурма такова. Собирается группа лиц, отобранных для генерации альтернатив: главный принцип отбора - разнообразие профессий, квалификации, опыта - такой принцип поможет расширить фонд априорной информации, которой располагает группа. Сообщается, что приветствуются любые идеи, возникшие как индивидуально, так и по ассоциации при выслушивании предложений других участников, в том числе и лишь частично улучшающие чужие идеи. Категорически запрещается любая критика - это важнейшее условие мозгового штурма: сама возможность критики тормозит воображение. Каждый по очереди зачитывает свою идею, остальные слушают и записывают на карточки новые мысли, возникшие под влиянием услышанного. Затем все карточки собираются, сортируются и анализируются, обычно другой группой экспертов. Общий «выход» такой группы, где идея одного может навести другого на что-то еще, часто оказывается больше, чем общее число идей, выдвинутых тем же количеством людей, но работающих в одиночку. Число альтернатив можно впоследствии увеличить, комбинируя сгенерированные идеи. Среди полученных в результате мозгового штурма идей может оказаться много неосуществимых, но «глупые» идеи легко исключаются последующей критикой, ибо компетентная критика проще, чем компетентное творчество [62, 126, 257 и др.].
  Метод мозгового штурма известен также под названием «мозговой атаки», коллективной генерации идей (КГИ), конференции идей, метода обмена мнениями.
  В зависимости от принятых правил и жесткости их выполнения различают прямую мозговую атаку, метод обмена мнениями, метод типа комиссий, судов (в последнем случае создаются две группы: одна вносит как можно больше предложений, а вторая старается максимально их раскритиковать). Мозговую атаку можно проводить в форме деловой игры, с применением тренировочной методики «стимулирования наблюдения», в соответствии с которой группа формирует представление о проблемной ситуации, а эксперту предлагается найти наиболее логичные способы решения проблемы.
  На практике подобием мозгового штурма могут явиться заседания совещательных органов разного рода - директораты, заседания ученых и научных советов, педагогические советы, специально создаваемые комиссии и т.д.
  Метод «Делфи» или метод «дельфийского оракула» является итеративной (повторяющейся) процедурой при проведении мозговой атаки, которая способствует снижению влияния психологических факторов и повышению объективности результатов. Основные средства повышения объективности результатов при применении метода «Делфи» - использование обратной связи, ознакомление экспертов с результатами предшествующего тура опроса и учет этих результатов при оценке значимости мнений экспертов.
  В конкретных методиках, реализующих процедуру «Делфи», эта идея используется в разной степени. Так, в упрощенном виде организуется последовательность итеративных циклов мозговой атаки. В более сложном варианте разрабатывается программа последовательных процедур анкетирования, исключающих контакты между экспертами, но предусматривающих ознакомление их с мнениями друг друга между турами.
  С примерами применения методов «Делфи» можно познакомиться в [235 и др.]. В силу трудоемкости обработки результатов и значительных временных затрат первоначально предусматриваемые методики «Делфи» не всегда удается реализовать на практике.
  В последнее время процедура «Делфи» в той или иной форме обычно сопутствует другим методам моделирования систем - методу «дерева целей», морфологическому и т.п.
  Метод синектики предназначен для генерирования альтернатив путем ассоциативного мышления, поиска аналогий поставленной задаче. В противоположность мозговому штурму здесь целью является не количество альтернатив, а генерирование небольшого числа альтернатив (даже единственной альтернативы), разрешающих данную проблему. Эффективность синектики была продемонстрирована при решении многих проблем типа «спроектировать усовершенствованный нож для открывания консервных банок», «изобрести более прочную крышу» и т.д. Известен случай синектического решения более общей проблемы экономического плана: «разработать новый вид продукции с годовым потенциалом продаж 300 млн. долларов». Известны попытки применения синектики в решении социальных проблем типа «как распределить государственные средства в области градостроительства».
  Суть метода синектики заключается в том, что формируется группа из 5-7 человек, отобранных по признакам гибкости мышления, практического опыта (предпочтение отдается людям, менявшим профессии и специальности), психологической совместимости, общительности. Группа ведет систематическое направленное обсуждение любых аналогий с подлежащей решению проблемой, спонтанно возникающих в ходе бесед. Перебираются и чисто фантастические аналогии.
  Особое значение синектика придает аналогиям, порождаемым двигательными ощущениями. Это вызвано тем, что наши природные двигательные рефлексы сами по себе высокоорганизованны и их осмысление может подсказать хорошую системную идею. Предлагается, например, поставить себя на место фантастического организма, выполняющего функцию проектируемой системы и т.п. Раскрепощенность воображения, интенсивный творческий труд создают атмосферу душевного подъема, характерную для синектики. Успеху работы синектических групп способствует соблюдение определенных правил, в частности: 1) запрещено обсуждать достоинства и недостатки членов группы; 2) каждый имеет право прекратить работу без каких-либо объяснений при малейших признаках утомления; 3) роль ведущего периодически переходит к разным членам группы и т.д.
  Наряду с перечисленными выше, в практике моделирования систем могут, очевидно, применяться и методы, используемые в экономике, управлении производством, а также в сферах обработки информации. Это, в частности, такие методы, как балансные методы, методы обычного планирования, календарного планирования, потоковые методы, методы массового обслуживания; методы работы с массивами информации (методы организации массивов, обработки массивов, методы поиска информации) и т.д. [29, 39, 58, 59].
  Количественные методы моделирования (математическое моделирование). Для исследования характеристик процесса функционирования любой системы математическими методами, включая и компьютерное моделирование, должна быть проведена формализация этого процесса, то есть построена математическая модель.
  Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта и требуемой достоверности и точности решения этих задач. Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности.
  Можно выделить следующие этапы построения математической модели (см. также Рис. 19).
  1. Определение предмета и цели моделирования, включая границы исследуемой системы и те основные свойства, которые должны быть отражены моделью (см. обсуждение соотношения объекта и предмета исследования, а также метода абстрагирования выше).
  2. Выбор языка (аппарата) моделирования. На сегодняшний день не существует общепризнанной классификации методов математического моделирования. Например, в [172] было предложено выделить оптимизационные и теорети- ко-игровые модели. Существуют несколько десятков «аппаратов» моделирования (см. сноски на настоящей странице и библиографические ссылки в них), каждый из которых представляет собой разветвленный раздел прикладной математики. Описывать всех их подробно в рамках настоящей книги не представляется возможным (да и целесообразным). В качестве примера проиллюстрируем, какого рода модели позволяет строить теория графов.
  Теория графов - раздел дискретной математики. Неформальное определение графа таково: графом называется совокупность вершин (изображаемых кружками) и связей между ними, изображаемых ориентированными дугами (со стрелками) или неориентированными ребрами (без стрелок) - см. Рис. 18.

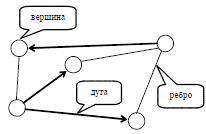
Рис. 18. Пример графа

  Язык графов оказывается удобным для моделирования многих физических, технических, экономических, биологических, социальных и других систем.
  Приведем ряд примеров приложений теории графов (более подробное описание перечисляемых и других задач можно найти в [26, 29]).
  а) «Транспортные» задачи, в которых вершинами графа являются пункты погрузки/разгрузки, а ребрами - дороги (автомобильные, железные и др.) и/или другие транспортные (например, авиационные) маршруты. Другой пример - сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства и потребления, а ребрами или дугами - возможные маршруты перемещения (линии электропередач, газопроводы, дороги и т.д.). Соответствующий класс задач оптимизации потоков грузов, размещения пунктов производства и потребления и т.д., иногда называется задачами обеспечения или задачами о размещении. Их подклассом являются задачи о грузоперевозках.
  б) «Технологические задачи», в которых вершины отражают производственные элементы (заводы, цеха, станки и т.д.), а дуги - потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.
  в) Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги - потоки материальных и финансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями.
  г) Управление проектами (см. также раздел 3.4). С точки зрения теории графов проект - совокупность операций и зависимостей между ними (сетевой график). Хрестоматийным примером является проект строительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).
  д) Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства, доверия, симпатии и т.д.) - в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности взаимодействия, и др.
  3. Выбор переменных, описывающих состояние системы и существенные параметры внешней среды, а также шкал их измерения и критериев оценки (см. также Рис. 15).
  4. Выбор ограничений, то есть множеств возможных значений переменных, и начальных условий (начальных значений переменных).
  5. Определение связей между переменными с учетом всей имеющейся о моделируемой системе информации, а также известных законов, закономерностей и т.п., описывающих данную систему. Именно этот этап иногда называют «построение модели» (в узком смысле).
  6. Исследование модели - или имитационное, или/и применение методов оптимизации и, быть может, решение задачи управления (см. описание каждого из этих трех блоков ниже). Именно этот этап иногда называют «моделированием» (в узком смысле).
  7. Изучение устойчивости и адекватности модели (см. ниже).
  Последующие этапы, связанные с практической реализацией модели и/или внедрением результатов моделирования, мы здесь не рассматриваем.
  Приведенные этапы математического моделирования иногда приходится повторять, возвращаясь к более ранним этапам при уточнении цели моделирования, обеспечении точности, устойчивости, адекватности и т.д. Рассмотрим два примера, иллюстрирующих приведенные выше семь этапов построения математической модели.
  В качестве первого примера возьмем задачу проектирования устройства полива клумбы заданного радиуса. Движение струи воды адекватно описывается известной из школьного учебника по физике моделью движения тела, брошенного под углом к горизонту.
  1. Предметом моделирования является движение тела, брошенного под углом к горизонту (струи воды). Целью является описание этого движения. При этом мы абстрагируемся от размеров и других свойств этого тела (диаметра струи), пренебрегаем сопротивлением воздуха.
  2. В качестве «аппарата» моделирования используются дифференциальные уравнения (в школьном курсе физики - известные их решения).
  3. В качестве переменных, описывающих состояние системы, используются координаты тела по горизонтали - x(t) и по вертикали - y(t), измеренные, например, в системе отсчета, связанной с поверхностью Земли.
  4. Считается, что известны начальные координаты устройства полива - (х0, y0) и вектор начальной скорости струи воды (V₀^X, V₀^Y).
  5. Известно, что на любое тело, находящееся в поле тяготения Земли, действует сила тяжести, сообщающее свободно движущемуся телу ускорение свободного падения g, направленное к центру Земли. Записав второй закон Ньютона, получаем уравнения движения:

  6. Исследование модели заключается в нахождении дальности полива L, то есть расстояния по горизонтали, которое пролетит тело (струя воды). Пусть для простоты устройство полива расположено на поверхности Земли (y0 = 0), тогда, приравняв y(t) нулю, находим время движения струи: T = 2 V₀^Y /g. Подставляя это время в выражение для x(t), получим выражение для дальности полива:

  7. Данная модель устойчива (например, дальность полива непрерывно зависит от вертикальной и горизонтальной составляющих начальной скорости струи, и малые ошибки в их определении приведут к малым ошибкам в вычислении дальности).
  В качестве второго примера рассмотрим так называемую дуополию Курно, описывающую конкуренцию двух экономических агентов.
  1. Предметом моделирования является взаимодействие двух агентов - производителей одного и того же товара, - каждый из которых выбирает свой объем производства (предложение товара), стремясь максимизировать свою прибыль в условиях, когда рыночная цена убывает с ростом суммарного предложения. Целью моделирования является предсказание рыночного равновесия - объемов производства и цены.
  2. В качестве «аппарата» моделирования используется теория некооперативных игр [55].
  3. В качестве переменных, описывающих состояние системы, выберем неотрицательные объемы производства х1 и х2 соответственно первого и второго агентов и рыночную цену Р.
  4. Считается, что известны:
  - зависимость цены: p = 5 - (х1 + х2) от суммарного предложения х1 + х2 - чем больше предложение, тем ниже цена;
  - затраты 3 (х1)² и 5 (х2)² / 4 соответственно первого и второго агентов - чем больше объем выпуска, тем выше затраты;
  5. Прибыль каждого агента представляет собой разность между его выручкой (равной произведению цены на его объем производства) и затратами, то есть целевые функции первого и второго агентов равны соответственно
  [5 - (х1 + х2)] х1 - 3 (х1)² и
  [5 - (х1 + х2)] х2 - 5 (х2)² / 4.
  6. Исследование модели заключается в нахождении объемов производства х*1 и х*2 , максимизирующих прибыли агентов (точнее - в нахождении так называемого равновесия Нэша (то есть, таких объемов производства, одностороннее отклонение от которых не выгодно ни одному из агентов) их игры [55]): х*1 = 0,5, х*2 = 1 и вычислении соответствующей рыночной цены, равной 3,5.
  7. Данная модель устойчива (например, малые ошибки в измерении коэффициентов затрат агентов приведут к малым ошибкам в вычислении равновесной цены).
  Завершив рассмотрение примеров, отметим, что математическое моделирование можно разделить на аналитическое и имитационное [172, 226].
  Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (например, уравнений - алгебраических, дифференциальных, интегральных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами:
  - аналитическим, когда стремятся получить в общем (аналитическом) виде явные зависимости для искомых характеристик в виде определенных формул. Оба рассмотренных выше примера построения математической модели были исследованы аналитически;
  - численным, когда, не имея возможности решать уравнения в общем виде, стремятся получить числовые результаты при тех или иных конкретных начальных данных (например, с помощью компьютера);
  - качественным, когда, не имея решения в явном виде, можно найти некоторые его свойства. Примером могут служить так называемые «мягкие» модели [8], в которых анализ вида дифференциальных уравнений, описывающих самые разнообразные процессы (экономические, экологические, политические и др.) позволяет делать качественные выводы о свойствах их решений - существовании и типе равновесных точек, областях возможных значений переменных и т. п.
  Для имитационного моделирования характерно исследование отдельных траекторий динамики моделируемой системы. При этом фиксируются некоторые начальные условия (начальное состояние системы или параметры модели) и рассчитывается одна траектория. Затем выбираются другие начальные условия, и рассчитывается другая траектория и т.д. То есть, аналитической зависимости между параметрами модели и будущими состояниями системы не ищется. Как правило, при имитационном моделировании используют численные методы, реализованные на компьютере. Плюс имитационного моделирования заключается в том, что оно позволяет проанализировать различные сценарии иногда даже для очень сложных моделей. Его недостаток состоит в отсутствии возможности получения, например, ответа на вопрос, в каких случаях (при каких значениях начальных условий и параметров модели) динамика системы будет удовлетворять заданным требованиям. Кроме того, обычно затруднителен анализ устойчивости имитационных моделей.
  Итак, мы кратко рассмотрели вопрос о построении моделей, в том числе - математических (обсуждение устойчивости и адекватности моделей, а также связанных с моделями проблем оптимизации и задач управления, производится ниже). Тех читателей, которые заинтересуются современными способами формализованного представления моделей, мы отсылаем к достаточно полным их описаниям, выполненным для ряда предметных областей в [26, 29, 39, 44, 55, 59, 126, 150, 172, 176, 182, 192, 198, 217].
  Отметим, что, несмотря на то, что на сегодняшний день накоплен значительный опыт разработки и использования самых разных методов моделирования (в том числе - математического), все равно в этом процессе решающую роль играет творчество, интуитивное искусство создания модели.
  Следующий этап стадии моделирования - оптимизация.
  Этап оптимизации. Оптимизация заключается в том, чтобы среди множества возможных вариантов (моделей проектируемой системы) найти наилучшие в заданных условиях, при заданных ограничениях, то есть оптимальные альтернативы. В этой фразе важное значение имеет каждое слово. Говоря «наилучшие», мы предполагаем, что у нас имеется критерий (или ряд критериев), способ (способы) сравнения вариантов. При этом важно учесть имеющиеся условия, ограничения, так как их изменение может привести к тому, что при одном и том же критерии (критериях) наилучшими окажутся другие варианты.
  Понятие оптимальности получило строгое и точное представление в различных математических теориях, прочно вошло в практику проектирования и эксплуатации технических систем, сыграло важную роль в формировании современных системных представлений, широко используется в административной и общественной практике, стало понятием, известным практически каждому человеку. Это и понятно: стремление к повышению эффективности труда, любой целенаправленной деятельности как бы нашло свое выражение, свою ясную и понятную форму в идее оптимизации.
  В математическом смысле суть оптимизации, вкратце, заключается в следующем. Пусть состояние моделируемой системы определяется совокупностью показателей: x = (x1, x2, x3, ..., xn), принимающих числовые значения. На множество возможных состояний системы наложено ограничение: x ∈ X, где множество X определяется существующими физическими, технологическими, логическими, ресурсными и другими ограничениями. Далее вводится функция F(x), зависящая от x1, x2, x3, ..., xn, которая называется критерием эффективности и принимает числовое значение. Считается, что чем большие значения принимает функция F(x), тем выше эффективность, то есть, тем «лучше» состояние x системы.
  Задача оптимизации заключается в нахождении оптимального значения x*, то есть допустимого состояния системы (x ∈X), имеющего максимальную эффективность: для всех x из множества X выполняется F(x*) ≥ F(x).
  Приведем пример простейшей задачи оптимизации. Пусть имеется R единиц ресурса, и n инвестиционных проектов. Каждый проект характеризуется отдачей ai > 0 на единицу вложенных средств. Величина xi ≥ 0 описывает, какое количество ресурса инвестируется в i-ый проект. Множеством X в данном примере будет множество таких векторов инвестиций, сумма компонентов которых не превосходит бюджетного ограничения: x1 + x2 + x3 + ... + xn ≤ R, то есть, допустимы любые комбинации инвестиций, удовлетворяющих ограничению на первоначальное количество ресурса. Критерием эффективности естественно считать суммарную отдачу от инвестиций: F(x) = a1 х1 + a2 х2 +... + an xn. Оптимальным в данном примере будет вложение всех средств в тот инвестиционный проект, который характеризуется максимальной отдачей на единицу вложенных средств (с максимальным значением аг).
  Такой вывод вполне соответствует здравому смыслу, и для его получения вряд ли стоило формулировать математическую задачу оптимизации. Однако, если усложнить модель (например, учесть риск или тот факт, что проекты могут требовать фиксированных инвестиций и давать фиксированную отдачу, и т.п.), то задача станет не столь тривиальной и без оптимизационных моделей нельзя будет обойтись (см. примеры в [26, 29]). Например, пусть имеются 100 единиц ресурса и два проекта. У первого проекта отдача на единицу вложенных средств равна 1,8, у второго - 1,4. Вероятность успешного завершения первого проекта равна 0,85, второго - 0,95. Требуется распределить инвестиции между проектами так, чтобы ожидаемый доход был максимален: 1,8-0,85 . х1 + 1,4-0,95 . х2 → max, при условии, что расходуется количество ресурса, не большее имеющегося: х1 + х2 ≤ 100, и ожидаемые потери не должны превышать 9 % от имеющегося ресурса: (1 - 0,85) . х1+ (1 - 0,95) . х2 ≤ 9. Данная оптимизационная задача (являющаяся задачей линейного программирования [201]) имеет следующее решение: х*1 = 40, х*2 = 60. Значение критерия эффективности при этом равно 141.
  Отметим, что при постановке и решении оптимизационных задач существенное значение имеет выбор критерия эффективности и ограничений. Так, если в рассмотренном выше примере в ограничении на ожидаемые потери заменить 9 % на 11 %, то оптимальным будет совсем другое решение: х*1 = 60, х*2 = 40. Другим (равным 145) станет и значение критерия эффективности.
  Мы привели простейший пример задачи оптимизации. Читателей, заинтересованных в более подробном изучении теории оптимизации, отсылаем к [26, 27, 29, 44, 55, 150, 172, 192, 201, 217] и спискам литературы в этих источниках.
  Различие между строго научным, математизированным и «общепринятым», житейским пониманием оптимальности, в общем-то, невелико [192]. Правда, нередко встречающиеся выражения вроде «более оптимальный», строго говоря, некорректны (нельзя достичь эффективности, больше максимальной). Но люди, использующие эти выражения, на самом деле просто нестрого и неудачно выражают правильную мысль: как только дело касается конкретной оптимизации, они достаточно легко исправляют формулировки.
  Если не вдаваться в подробности оптимизации в рамках математических моделей, то интуитивно оптимизация сводится, в основном, к сокращению числа альтернатив и проверке модели на устойчивость.
  Если специально стремиться к тому, чтобы на начальной стадии было получено как можно больше альтернатив, то для некоторых проблем их количество может достичь большого числа возможных решений. Очевидно, что подробное изучение каждой из них приведет к неприемлемым затратам времени и средств. На этапе неформализованной оптимизации рекомендуется проводить «грубое отсеивание» альтернатив, проверяя их на присутствие некоторых качеств, желательных для любой приемлемой альтернативы. К признакам «хороших» альтернатив относятся надежность, многоцелевая пригодность, адаптивность, другие признаки «практичности». В отсеве могут помочь также обнаружение отрицательных побочных эффектов, недостижение контрольных уровней по некоторым важным показателям (например, слишком высокая стоимость) и пр. Предварительный отсев не рекомендуется проводить слишком жестко; для детального анализа и дальнейшего выбора необходимы хотя бы несколько альтернативных вариантов.
  Важным требованием, предъявляемым к моделям, является требование их устойчивости при возможных изменениях внешних и внутренних условий, а также устойчивости по отношению к тем или иным возможным изменениям параметров самой модели проектируемой системы. Проблемам устойчивости математических моделей систем посвящена довольно обширная литература (см., например, [150, 182, 192 и др]).
  Для того чтобы понять роль устойчивости, вернемся (см. также выше) к рассмотрению процесса построения математической модели некоторой реальной системы и проанализируем возможные «ошибки моделирования» [170]. Первым шагом является выбор того «языка», на котором формулируется модель, то есть того математического аппарата, который будет использоваться (горизонтальная пунктирная линия на Рис. 19 является условной границей между реальностью и моделями). Как правило, этот этап характеризуется высоким уровнем абстрагирования - выбираемый класс моделей намного шире, чем моделируемый объект. Возможной ошибкой, которую можно совершить на этом шаге, является выбор неадекватного языка описания.
  Следующим этапом по уровню детализации является построение множества частных моделей, при переходе к которым вводятся те или иные предположения относительно свойств параметров модели. Возникающие здесь ошибки описания структуры модели могут быть вызваны неправильными представлениями о свойствах элементов моделируемой системы и их взаимодействии.
  После задания структуры модели посредством выбора определенных значений параметров (в том числе - числовых) происходит переход к некоторой конкретной модели, которая считается аналогом моделируемого объекта. Источник возникающих на этом этапе «ошибок измерения» очевиден, хотя он и имеет достаточно сложную природу и заслуживает отдельного обсуждения.

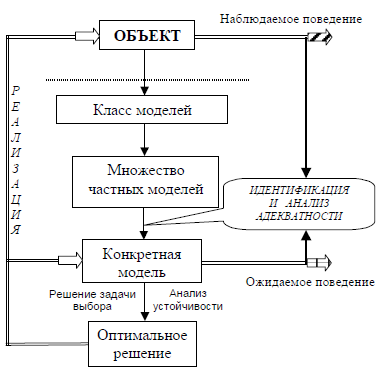
Рис. 19. Этапы построения и исследования математической модели

  Когда для конкретной модели решается задача выбора оптимальных решений, то, если существует аналитическое решение для множества частных моделей, тогда, как правило, частные значения параметров, соответствующие конкретной модели, подставляются в это решение. Если аналитического решения не существует, то оптимальное решение ищется посредством имитационных экспериментов с привлечением вычислительной техники. На этом этапе - при численных расчетах - возникают вычислительные ошибки.
  Изучение устойчивости решений в большинстве случаев сводится к исследованию зависимости оптимального решения от параметров модели. Если эта зависимость является непрерывной, то малые ошибки в исходных данных приведут к небольшим изменениям оптимального решения. Тогда, решая задачу выбора по приближенным данным, можно обоснованно говорить о нахождении приближенного решения.
  Обсудим теперь, что следует понимать под адекватностью модели. Для этого вернемся к Рис. 19. Оптимальное решение, полученное для конкретной модели, является оптимальным в том смысле, что при его использовании поведение модели соответствует предъявляемым требованиям. Рассмотрим, насколько обоснованным является использование этого решения в реальной системе - моделируемом объекте.
  Наблюдаемое поведение модели является с точки зрения субъекта, осуществляющего моделирование (например, полагающего, что модель адекватна), предполагаемым поведением реальной системы, которое в отсутствии «ошибок моделирования» будет оптимально в смысле выбранного критерия эффективности. Понятно, что в общем случае наблюдаемое поведение реальной системы и ее предполагаемое поведение могут различаться достаточно сильно. Следовательно, необходимо исследование адекватности модели, то есть - устойчивости поведения не модели, а реальной системы относительно ошибок моделирования (см. Рис. 19).
  Действительно, представим себе следующую ситуацию. Пусть построена модель и найдено оптимальное в ее рамках решение. А что будет, если параметры модели «немного» отличаются от параметров реальной системы? Получается, что задача выбора решалась не для «той» системы. Отрицать такую возможность, естественно, нельзя. Поэтому необходимо получить ответы на следующие вопросы:
  - насколько оптимальное решение чувствительно к ошибкам описания модели, то есть, будут ли малые «возмущения» модели приводить к столь же малым изменениям оптимального решения (задача анализа устойчивости);
  - будут ли решения, обладающие определенными свойствами в рамках модели (например, оптимальность, эффективность не ниже заданной и т. д.), обладать этими же свойствами и в реальной системе, и насколько широк класс реальных систем, в которых данное решение еще обладает этими свойствами (задача анализа адекватности).
  Качественно, основная идея, используемая на сегодняшний день в математическом моделировании, заключается в следующем [151, 170]. Применение оптимальных решений приводит к тому, что они, как правило, оказываются неоптимальными при малых вариациях параметров модели. Возможным путем преодоления этого недостатка является расширение множества «оптимальных» решений за счет включения в него так называемых приближенных решений (то есть, «немного худших», чем оптимальные). Оказывается, что ослабление определения «оптимальность» позволяет, установив взаимосвязь между возможной неточностью описания модели и величиной потерь в эффективности решения, гарантировать некоторый уровень эффективности множества решений в заданном классе реальных систем, то есть расширить область применимости решений за счет использования менее эффективных из них. Иными словами, вместо рассмотрения фиксированной модели реальной системы, необходимо исследовать семейство моделей.
  Приведенные качественные рассуждения свидетельствуют, что существует определенный дуализм между эффективностью решения и областью его применимости (областью его устойчивости и/или областью адекватности).
  В практике же проектирования систем, так же как и во многих других областях профессиональной деятельности, не поддающихся пока «математизации», для оптимизации используются такие методы, как анализ, «проигрывание» возможных ситуаций, «мысленный эксперимент» (что произойдет, если изменяются такие-то условия? такие-то условия? и т.д.).
  Отобранные и проверенные на устойчивость и адекватность модели становятся основой для последнего, решающего этапа стадии моделирования - выбора модели для дальнейшей реализации.
  Этап выбора модели (принятия решения). Выбор одной - единственной - модели для дальнейшей реализации является последним и, пожалуй, наиболее ответственным этапом стадии моделирования, его завершением.
  Выбор является действием, придающим всей деятельности целенаправленность. Именно выбор реализует подчиненность всей деятельности определенной цели. Рано или поздно наступает момент, когда дальнейшие действия могут быть различными, приводящими к разным результатам, а реализовать можно только одно. Причем вернуться к исходной ситуации, как правило, уже невозможно.
  Способность сделать правильный выбор в таких условиях - ценное качество, которое присуще разным людям в разной степени. Великие полководцы, политики, ученые и инженеры, талантливые администраторы отличались и отличаются от своих коллег-конкурентов, в первую очередь, умением делать лучший выбор, принимать правильное решение.
  В системном анализе выбор (принятие решения) [192 и др.] определяется как действие над множеством альтернатив, в результате которого получается подмножество выбранных альтернатив (обычно это один вариант, одна альтернатива, но не обязательно). При этом выбор тесно связан с оптимизацией, так как последняя есть ни что иное, как выбор оптимальной альтернативы.
  Каждая ситуация выбора может развертываться в разных вариантах:
  - оценка альтернатив для выбора может осуществляться по одному или нескольким критериям, которые, в свою очередь, могут иметь как количественный, так и качественный характер;
  - режим выбора может быть однократным (разовым) или повторяющимся, допускающим обучение на опыте;
  - последствия выбора могут быть точно известны (выбор в условиях определенности), иметь вероятностный характер (выбор в условиях риска), или иметь неопределенный исход (выбор в условиях неопределенности);
  - ответственность за выбор может быть односторонней (в частном случае индивидуальной - например, ответственность директора организации, учреждения) или многосторонней (например, когда за решение несут, а чаще всего не несут никакой ответственности разрозненные ведомства - от муниципального до федерального уровня - типичный случай нашей традиционной российской «коллективной безответственности»). Соответственно различают индивидуальный или групповой, многосторонний выбор;
  - степень согласованности целей при многостороннем выборе может варьироваться от полного совпадения интересов сторон до их полной противоположности (выбор в конфликтной ситуации). Возможны также промежуточные случаи, например, компромиссный выбор, коалиционный выбор, выбор в условиях конфликта и т.д.
  Получить первоначальное представление о математических моделях выбора (принятия решений) можно из [1, 55, 127, 192, 217].
  Как правило, выбор рационального варианта модели проектируемой системы основывается на последовательном сокращении числа рассматриваемых вариантов за счет анализа и отбрасывания неконкурентоспособных по различным соображениям и показателям альтернатив. При выборе альтернатив следует иметь в виду, что цели проектируемой системы могут быть подразделены по их приоритетности на:
  - цели, достижение которых определяет успех проекта;
  - цели, которыми частично можно пожертвовать для достижения целей первого уровня;
  - цели, имеющие характер дополнения.
  В любом случае выбор (принятие решения) является процессом субъективным, и лицо (лица), принимающие решение, должны нести за него ответственность. Поэтому в целях преодоления (уменьшения) влияния субъективных факторов на процесс принятия решения используются чаще всего методы экспертизы. В литературе имеется большое разнообразие методов экспертной оценки: [39, 126, 127, 221 и др.]. Наиболее простыми из них являются метод комиссий и метод суда.
  Метод комиссий состоит в открытой дискуссии по обсуждаемой проблеме для выработки единого мнения экспертов. Коллективное мнение определяется в результате открытого или тайного голосования. В некоторых случаях к голосованию не прибегают, выявляя результирующее мнение в процессе дискуссии. Преимущества метода комиссий: возможен рост информированности экспертов, поскольку при обсуждении эксперты приводят обоснование своих оценок, и обратная связь - под воздействием полученной информации эксперт может изменить первоначальную точку зрения.
  Однако метод комиссий обладает и недостатками. К их числу, прежде всего, относится отсутствие анонимности. Оно может приводить к достаточно сильным проявлениям конформизма со стороны экспертов, присоединяющих свои мнения к мнению более компетентных и авторитетных экспертов даже при наличии противоположной собственной точки зрения. Дискуссия часто сводится к полемике наиболее авторитетных экспертов. Существенным фактором становится и различная активность экспертов, не всегда коррелированная с их компетентностью. Кроме того, публичность высказываний может приводить к нежеланию некоторых экспертов отказаться от ранее высказанного мнения, даже если оно в процессе дискуссии претерпело изменения.
  Экспертиза по методу суда использует аналогии с судебным процессом. Часть экспертов объявляется сторонниками рассматриваемой альтернативы и выступает в качестве защиты, приводя доводы в пользу рассматриваемой альтернативы. Часть экспертов объявляется ее противниками и пытается выявить отрицательные стороны. Часть экспертов регулирует ход экспертизы и выносит окончательное решение. В процессе экспертизы по методу суда «функции» экспертов могут меняться. Метод суда обладает теми же преимуществами и недостатками, что и метод комиссий.
  Применяются также и другие методы экспертизы: методы предпочтений, попарных сравнений, смешанной альтернативы, согласования оценок и т.д., а также методы сложных экспертиз, например метод решающих матриц и др. [39, 126, 127, 217, 221].
  Кроме того, дополнительно используются еще и методы оценки качества экспертиз [126]. Ведь для проведения экспертиз должны быть отобраны компетентные эксперты, хорошо знакомые с предметом экспертизы, обладающие достаточным опытом, способные выносить обоснованные объективные суждения.
  1. Документационный метод предполагает оценку качества эксперта на основании таких документальных данных, как число публикаций и ссылок на работы эксперта, ученая степень, стаж, успешность карьеры, занимаемая должность и т.д.
  2. Тестовый метод предполагает отбор экспертов на основании решения ими тестовых задач, в которых отражена специфика предмета экспертизы. В качестве теста могут также рассматриваться результаты участия эксперта в аналогичных экспертизах.
  3. Достаточно часто используются методы взаимооценки и самооценки экспертов. Взаимооценка осуществляется, как правило, двумя способами. В первом из них каждый предполагаемый член экспертной комиссии оценивает компетентность, объективность и т.д. других предполагаемых экспертов. Во втором - оценку качества предполагаемых экспертов осуществляет аналитическая группа, которой поручена организация и проведения экспертизы. При самооценке определение степени знакомства с предметом экспертизы, компетентности и т.д. в достаточно детализированном виде осуществляется самим экспертом. Взаимооценка и самооценка экспертов может носить как качественный, так и количественный характер.
  4. Метод оценки непротиворечивости суждений эксперта. Опыт проведения экспертиз показывает, что эксперт далеко не всегда последователен в своих оценках. Особенно часто непоследовательность экспертов проявляется при использовании метода парных сравнений. Так, например, эксперт может считать альтернативу «а» более предпочтительной, чем «б», альтернативу «б» - более предпочтительной, чем «в», и вместе с тем альтернативу «в» - более предпочтительной, чем «а». Такая непоследовательность объясняется различными причинами. С одной стороны, решающее влияние может оказывать специфика проводимой экспертизы, наличие сложной многокритериальной системы предпочтений у эксперта. С другой стороны, причиной непоследовательности эксперта может служить недостаточное его знакомство с предметом экспертизы, недостаточно четкая формулировка вопросов, обращенных к эксперту, отсутствие четкого представления о цели экспертизы. Выявить конкретные причины непоследовательности эксперта может лишь специально проведенный анализ.
  Таким образом, по принятии решения о выборе модели завершается стадия моделирования системы. Далее следует стадия ее конструирования.
  СТАДИЯ КОНСТРУИРОВАНИЯ СИСТЕМ. Следующей стадией фазы проектирования систем является стадия конструирования, которая заключается в определении конкретных способов и средств реализации выбранной модели в рамках имеющихся условий.
  Если проводить аналогию с техникой, то этот этап при создании, например, автомобиля, самолета и т.д. будет заключаться в том, что на основе созданной концептуальной модели проекта начинается конструирование конкретных узлов и механизмов будущей машины, увязанных, согласованных между собой и в совокупности своей позволяющих в дальнейшем реализовать «в металле» концептуальную модель.
  Процесс конструирования включает в себя этапы: декомпозиции, агрегирования, исследования условий, построения программы [39, 192 и др.].
  Этап декомпозиции. Декомпозиция - это процесс разделения общей цели проектируемой системы на отдельные подцели-задачи в соответствии с выбранной моделью. В этом отношении декомпозиция аналогична процессу формулирования задач в научном исследовании: там задачи формулируются как цели решения отдельных подпроблем в соответствии с определенной общей целью исследования и построенной гипотезой. В то же время имеется и принципиальное отличие: исследователь находится как бы в положении некой «робинзонады» - ведь он манипулирует с объектом, предметом своего исследования один (даже при коллективной форме организации исследований у него есть, как правило, собственный предмет исследования), и исследователь обладает определенной свободой выбора, свободой маневра. В практической же деятельности дело обстоит гораздо сложнее - специалистам-практикам приходится решать весь комплекс возникающих задач, что называется, «в лоб».
  Декомпозиция в иерархических системах предусматривает разделение общей цели на подцели (задачи), те, в свою очередь, разделяются на подзадачи и т.д. [132].
  Декомпозиция позволяет расчленить всю работу по реализации модели на пакет детальных работ, что делает возможным решение вопросов их рациональной организации, мониторинга, контроля и т. д.
  Основные правила декомпозиции заключаются в следующем:
  1. Как правило, реализуется два противоположных подхода:
  - подход «сверху» - целевой (целенаправленный) - для определения, как конкретная задача отвечает, согласуется с общей целью проекта (в соответствии с выбранной моделью);
  - подход «снизу» - морфологический - для определения конкретных возможностей реализации задачи: по ресурсному обеспечению, по временным и пространственным возможностям, по квалификации работников и т. п.
  2. Число задач в индивидуальном проекте или число компонентов каждой задачи коллективного проекта не должно быть больше так называемого числа Миллера 7 ± 2. Содержание этого требования можно объяснить ограничением возможностей оперативной памяти человека, его способностью анализировать в оперативной памяти не более 5^9 составляющих и связей между ними.
  3. Для каждой части проекта, соответствующей каждой задаче, определяются имеющие к ней отношение данные: продолжительность, объемы работ, необходимая информация, оборудование и т.д. и т.п.
  4. По каждой задаче проводится критический анализ для подтверждения правильности и выполнимости поставленной задачи.
  Этап агрегирования. Процесс, в определенном смысле противоположный декомпозиции - это агрегирование (дословно - соединение частей в целое). Для пояснения его сути приведем такой пример. Допустим, мы задумали создать самый современный автомобиль. Для этого возьмем самую лучшую и современную конструкцию инжектора, самую лучшую систему зажигания, самую лучшую коробку передач и т.д. А в результате не то что самого современного автомобиля, а даже просто автомобиля не получим - эти части, пусть самые лучшие и современные, не взаимосвязаны между собой. Таким образом, агрегирование - это процесс согласования отдельных задач реализации проекта между собой.
  В научном исследовании агрегирование как этап деятельности аналога не имеет.
  Основными методами агрегирования, если не брать в рассмотрение формальных математических моделей, являются определение конфигуратора и использование классификаций [192].
  Конфигуратором называется минимально достаточный набор различных языков описания процесса решения проблемы. Действительно, всякое сложное явление требует разностороннего, многопланового описания, рассмотрения с различных точек зрения. Только совместное (агрегированное) описание в понятиях нескольких качественно различающихся языков позволяет охарактеризовать явление с достаточной полнотой. Это соображение приводит к понятию агрегата, состоящего из качественно различных языков описания проектируемой системы и обладающего тем свойством, что число этих языков минимально, но необходимо для заданной цели. Этот агрегат и является конфигуратором [125].
  Поясним на примере. В электронике, радиотехнике для создания каждого прибора используется конфигуратор: блок- схема, принципиальная схема, монтажная схема. Блок-схема определяется теми техническими единицами, которые выпускаются промышленностью в виде готовых электронных блоков. Прибор членится на такие единицы. Принципиальная схема означает совершенное расчленение: она должна объяснить во всех подробностях функционирование этого прибора. Наконец, монтажная схема является результатом расчленения прибора в зависимости от геометрии объема прибора, в пределах которого производится сборка. Здесь главное в конфигураторе то, что синтез, проектирование, производство и эксплуатация прибора возможны только при наличии всех трех его описаний - любые два без третьего не имеют смысла.
  Этот пример дает возможность еще подчеркнуть зависимость конфигуратора от поставленных целей. Например, если конечной целью мы поставили не производство прибора, а его сбыт, продажу, то в конфигуратор придется включить еще и языки дизайна, рекламы, позволяющие описывать внешний вид и другие потребительские качества прибора.
  Другой пример. При описании процессов, происходящих в народнохозяйственных комплексах областного масштаба, было признано необходимым [191] для характеристики любого выходного продукта производственной и обслуживающей сферы использовать три типа показателей: натуральные (эко- номико-технологические), денежные (финансово-экономические) и социально-ценностные (идеологические, политические, этические и эстетические). Деятельность завода и театра, фермерского хозяйства и школы, любого предприятия и организации описывается на этих трех языках, образующих конфигуратор по отношению к целям автоматизированной системы управления хозяйством области.
  Третий пример. Опыт проектирования организационных систем [172] показывает, что для синтеза организационной системы конфигуратор состоит из описания распределения власти (системы подчиненности), распределения ответственности (структуры функционирования) и распределения информации (организация связи и памяти системы, накопления опыта, обучения, истории). Все три структуры не обязаны совпадать топологически, хотя связывают одни и те же части системы.
  Четвертый пример. В связи с идеей непрерывного образования - «образования через всю жизнь» возникает вопрос - какую языковую подготовку должна дать выпускнику общеобразовательная школа, чтобы он в дальнейшем имел возможность осваивать любую науку, любую деятельность? Общее образование должно дать ему знание языков:
  - родного языка, русского языка и иностранных языков как средства получения и переработки любой информации и как средства общения;
  - языка математики как универсального языка построения формальных моделей окружающей действительности, который может быть использован при изучении любой отрасли научного знания или при овладении любой профессиональной деятельностью;
  - языка информатики, который сегодня необходим любому человеку в любой сфере человеческой деятельности.
  Вот этот набор языков и является конфигуратором для построения содержания общего среднего образования в аспекте системы непрерывного образования.
  Отметим, что конфигуратор является содержательной моделью высшего возможного уровня. Перечислив языки, на которых мы будем говорить о системе, мы тем самым определяем, синтезируем тип системы, фиксируем наше понимание природы системы. Как всякая модель, конфигуратор имеет целевой характер и при смене цели может утратить свойства конфигуратора.
  Классификация как метод агрегирования. Простейший способ агрегирования состоит в установлении отношений эквивалентности между агрегируемыми элементами, то есть в образовании классов. Классификация и рассматривается как систематизация классов объектов, как средство установления связей между ними [254]. При этом класс может интерпретироваться как агрегированный представитель входящих в него элементов.
  Применение классификаций в целях упорядочения задач реализации проектируемой системы (а при иерархической их структуре - задач, подзадач и т.д.) позволяет выделить задачи как рядоположенные, равнозначные компоненты, поскольку они будут иметь общее основание классификации, сделав понятными связи между ними. Естественно, основания классификаций могут быть в каждом случае различными: по «пространственной» и временной структуре процесса реализации проекта, по составу, структуре и функциям (три основные характеристики, определяющие систему, если рассматривать каждую задачу как подсистему) и т.д.
  При иерархическом многоуровневом (более двух уровней) построении задач, естественно, возникает необходимость определения общего основания оснований классификаций. То есть, определение - по какому общему основанию строятся дальнейшие, более детальные классификации. Так, например, в [164] была выстроена трехуровневая система классификаций векторов развития российского образования, в [172] - четырехуровневая система классификаций моделей управления организационными системами. Существует множество известных иерархических классификаций - классификация биологических видов, общероссийский классификатор видов экономической деятельности и т.д. (см. также систему классификаций видов моделирования на Рис. 17).
  Между тем, и в практике проектирования систем, и в научных исследованиях, особенно по гуманитарным и общественным наукам (наукам слабой версии) отсутствие строгих классификаций является массовой болезнью - вместо использования строгих классификаций или построения собственных классификаций используются многочисленные «перечислиз- мы» - то есть никак не обоснованные совокупности свойств, качеств, характеристик и т.д. Так, например, в одном образовательном проекте была выделена следующая совокупность характеристик профессиональной деятельности учителя: «целенаправленность, функциональность, проблемность, динамичность, открытость и т.д.» Начать хотя бы с того, что в этом перечислении наличие аббревиатуры «и т.д.» означает, что подобную череду можно продолжать сколь угодно долго, например: структурность, технологичность, прогностичность, коммуникативность ... . И, опять же, в конце мы получим «... и т. д.». То есть никакого серьезного обоснования мы здесь не найдем - это просто типичный случай «перечислизмов». Но, как уже говорилось, «перечислизмы» на сегодня - массовая повсеместная болезнь. Хотя метод классификаций известен с древнейших времен.
  Мы рассмотрели два основных метода агрегирования: определение конфигуратора и использование классификаций.
  Существуют и другие методы агрегирования, основывающиеся на математических моделях. Так, существенным эффектом, возникающим в сложных иерархических системах, является агрегирование информации. Наличие агрегирования (сжатия) информации неизбежно присуще организационным иерархиям [167], агрегирование экономических и других показателей происходит в любых социально-экономических системах [183], в управлении проектами возникает необходимость агрегированного описания подпроектов [15, 99], в задачах управления нельзя обойтись без агрегированного описания состояний управляемой системы (так называемая задача комплексного оценивания) [172, 192] и т.д. Подробное описание используемых при этом формальных методов можно найти в литературе, ссылки на которую приведены выше.
  Таким образом, когда определена и выстроена вся взаимосвязанная совокупность задач реализации проекта (можно сказать, и это будет достаточно строго - система задач), начинается следующий этап конструирования системы - исследование условий.
  Этап исследования условий реализации модели. Естественно, любая модель проектируемой системы может быть реализована в практике лишь при наличии определенных условий. Полный перечень условий деятельности с их характеристиками мы приводили выше, в первой главе книги: кадровые, мотивационные, материально-технические, научно-методические, финансовые, организационные, нормативно-правовые, информационные условия (группы условий). Естественно, необходим детальный анализ по каждой задаче (по всей системе задач) и по каждой группе условий: какие конкретные условия имеются для решения каждой конкретной задачи, какие условия необходимо выполнить, создать дополнительно.
  Например, при анализе кадровых условий необходимо задаться вопросами:
  - какой опыт и какая квалификация требуется от сотрудника (исполнителя) для решения данной задачи?
  - хватает ли наличной квалификации сотрудника (сотрудников) для решения этой задачи или необходимо дополнительное обучение, повышение квалификации? В чем? Где? В каких объемах?
  - требуется ли опыт межличностного общения для эффективного решения задачи, такой, как опыт устного или письменного общения, дипломатичность, умение вести переговоры, потенциал и опыт руководителя?
  - как может быть организована работа сотрудника, в частности по должностным обязанностям и штатному расписанию?
  И так далее.
  Следует отметить, что в управлении проектами (см., например, [131] и раздел 3.4 настоящей работы) процедура исследования условий обычно именуется и рассматривается как исследование ресурсных возможностей. Как известно, ресурсами называются средства, запасы, возможности, источники чего-либо [227]. При этом выделяется семь видов ресурсов:
  - трудовые ресурсы;
  - деньги;
  - оборудование;
  - техническая оснастка;
  - материалы;
  - информация;
  - технологии.
  Думается, понятие «условия», во-первых, более общее и поглощает понятие «ресурсы». Кроме того, условия, очевидно, и более широкое понятие. Например, мотивационные условия вряд ли можно рассматривать как вид ресурсов.
  Естественно, такое разделение процесса конструирования системы на последовательные этапы: декомпозиция, агрегирование, исследование условий, несколько условно. Процесс осуществляется как бы «последовательно-параллельно»: и выделение задач, и их агрегирование постоянно соотносятся с реальными условиями их решения, агрегирование задач вызывает зачастую необходимость пересмотра их состава и т.д.
  Наконец, когда выстроена вся система задач реализации системы и исследованы условия ее реализации, приступают к последнему этапу конструирования системы - этапу построения программы реализации модели.
  Этап построения программы. Программа реализации модели системы на практике - это конкретный план действий по реализации модели в определенных условиях и в установленные (определенные) сроки.
  Построение программы начинается с операции «определения основных вех» [131]. Определение вех составляет начальную, наиболее обобщенную часть программы, которая потом развертывается в укрупненный и, наконец, в детальный план.
  При определении вех используется информация о ключевых точках, состояниях, через которые будет проходить процесс реализации модели системы на практике. Вехи отмечают существенные, определяющие дальнейший ход развития процесса точки перехода. Поэтому вехи позволяют решать проблемы контроля реализации системы, составляя набор естественных контрольных точек. При анализе выполнения работ вехи становятся эффективным средством управления (самоуправления), помогающим понять, на каком этапе находится процесс реализации проекта, оценить, достигнуты ли основные показатели состояния и сколько осталось времени, средств и конкретных работ до завершения проекта. Вехи не имеют продолжительности. Они используются в качестве дискретной шкалы, которая имеет всего две оценки - «выполнено» или «не выполнено». Так, например, при принятии решений по финансированию очередного этапа выполнения работ по договору вехи используются для оценки завершенности работ для выполнения платежей.
  Когда основные вехи определены, приступают к детальному планированию процесса реализации системы.
  Детальное планирование - это разработка детального графика (графиков в случае сложного проекта) выполнения работ по реализации системы. Детальный график, независимо от размеров проекта и его сложности, должен включать:
  - все ключевые события и даты;
  - точную последовательность работ. Логика их выполнения должна быть зафиксирована с помощью сетевого графика (сетевой диаграммы) - см. ниже. Сетевой график позволяет проследить все виды зависимостей между работами и взаимосвязь событий реализации;
  - график служит основой для определения этапов и прочих временных интервалов по реализации системы. Кроме того, он позволяет при необходимости определять потребности в ресурсах для каждой из частей, фрагментов или событий процесса реализации системы.
  Форма представления графика, естественно, произвольна. Но она должна быть удобна для пользования, в том числе - наглядна и понятна для всех участников реализации системы.
  Метод сетевого планирования. При разработке детального графика реализации системы наиболее удобным и часто используемым является метод сетевого планирования. Суть его заключается в построении сетевого графика, являющегося графическим отображением всех работ по реализации системы и зависимостей (в том числе временных и «пространственных») между ними. Сетевые графики строятся в виде графа (см. выше) - множества вершин, соответствующих работам, и связывающих их линий, представляющих взаимосвязи между работами: например, работа «Б» не может начаться раньше, чем завершится работа «А» (см. Рис. 20, а также описание диаграмм Ганта - Рис. 21) [26].

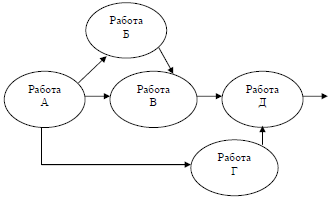
  Основная цель работы с сетевым графиком заключается в том, чтобы сократить до минимума продолжительность проекта (время реализации системы), в первую очередь - за счет выделения и минимизации так называемого «критического пути». Максимальный по продолжительности путь в сети, связывающий начальную (вершина «А» на Рис. 20) и конечную вершину (вершина «Д» на Рис. 20), называется критическим. Работы, лежащие на этом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность реализации системы в целом. Длительность процесса реализации проекта может быть сокращена за счет сокращения длительности работ, лежащих на критическом пути. Соответственно, любая задержка выполнения работ критического пути повлечет увеличение длительности процесса реализации системы. При этом анализу подлежат не только работы критического пути, но в той или иной степени близкие к нему, так как подобные работы даже при самом незначительном изменении графика могут стать критическими и существенно изменить сроки реализации системы. Для оптимизации сетевых графиков применяют методы календарно-сетевого планирования и управления (КСПУ), основная идея которых заключается в следующем. Предположим, что время выполнения работ зависит от задействованных на них ресурсов. Количество ресурсов ограничено. Требуется решить оптимизационную задачу - распределить ограниченные ресурсы между работами проекта таким образом, чтобы он был завершен за минимальное время. Методы решения этой и подобных задач подробно описаны в [26, 29, 99].
  При разработке детального графика реализации спроектированной системы удобно также использовать так называемую диаграмму Ганта - горизонтальную линейную диаграмму, на которой задачи реализации системы представляются протяженными во времени отрезками, характеризующимися календарными датами начала и окончания выполнения работ, а также, возможно, другими временными параметрами и, быть может, указанием взаимосвязи работ, используемых в них ресурсов и т.д. Пример диаграммы Ганта для такого организационного проекта, как проведение научной конференции, приведен на Рис. 21.

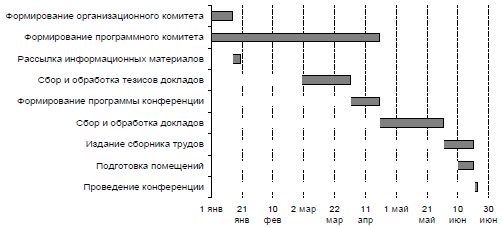
Рис. 21. Временной график организации научной конференции (диаграмма Ганта)

  На Рис. 21 работы изображены горизонтальными прямоугольниками, пунктиром обозначены временные этапы. Здесь важно подчеркнуть то обстоятельство, что исполнители по тем работам, которые невозможно начать сразу, не дождавшись результатов предыдущих работ, не должны ждать, ничего не предпринимая. Они могут плодотворно использовать это время для планирования своей деятельности. Кроме того, несколько работ могут выполняться параллельно, если для этого хватает ресурсов.
  Существенная особенность составления сетевого графика заключается в том, что он планируется с обеих сторон - и с начала, и с конца. Руководитель проекта, определив список работ (обеспечивающих достижение цели проекта), первым делом задается вопросами: когда следует получить все необходимые результаты (с учетом взаимозависимости работ), и когда могут быть реально получены эти результаты. И затем от баланса этих сроков в первом приближении прикидывается, в какой последовательности выполнять работы, когда следует начинать ту или иную работу, и когда она должны закончиться.
  Разработкой детального плана-графика работ по реализации завершается стадия конструирования системы.
  СТАДИЯ ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКИ. Последняя стадия фазы проектирования систем - стадия технологической подготовки процесса реализации спроектированной системы в практике. Она заключается в подготовке рабочих материалов, необходимых для реализации спроектированной системы: учебно-программной документации, методических разработок, программного обеспечения и т.д., а также, например, должностных инструкций исполнителей при реализации сложного проекта и т. п. Поскольку технологическая подготовка процесса реализации системы целиком определяется его конкретным содержанием и в каждом конкретном случае она специфична, и подробно описать эту стадию в общем виде вряд ли возможно.
  Таким образом, мы рассмотрели всю последовательность проектирования систем во всей ее полноте. Естественно, в простых случаях вовсе необязательно выполнять весь этот набор процедур. Если, к примеру, учитель проектирует очередной урок, или хирург планирует очередную операцию, то, конечно же, большинство стадий и этапов процесса проектирования будет пропущено, свернуто, или будет осуществляться на интуитивном уровне. Но чем сложнее проект, чем больше заинтересованных участников он охватывает, тем все больше проектирование будет «вписываться» в эту общую схему.
  Далее, согласно логике настоящей работы, мы рассмотрим следующую фазу проекта как формы организации практической деятельности - технологическую фазу.